딥러닝 공부 - 신경망 첫걸음 정리

어떤 강의를 들을지 모르겠다..

이 책은 전에 읽었던 책이고, 다시 복습하는 차원에서 필요한 것만 정리하겠다.

우선 신경망의 개념을 익히는 단계에서, 많은 예시를 들었다. 핵심적으로 다룬 것은 선형분류자, 오차, 학습률이다.

1. 선형함수

선형함수 : 선이 아닐 지라도 직선의 특징을 가지고 있다는 것이고 여기서 말하는 직선의 특징은 중첩의 원리(principle of superposition)또는 선형성의 원리(Linearity principle)이다. 일차함수를 생각하면 될 것이다. 단, 선형함수는 부모집단이고, 일차함수는 자식함수다.

선형분류자 : 선형으로된 분류자. (기울기를 통해 분류하고 나누는 분류자, 기울기를 조절하여 최적의 분류자를 도출한다.)

2. E = T(Target) - ax(선형분류자, 선형함수꼴)

--->

E= (a+ delta a)x - ax = (delta a)x  : delta a는 T에 도달하기 위한 조정 값

---> 

E/x= delta a

Ex> E=0.35, x=3.0 --> delta a= E/x= 0.1167

그러나, 목표값을 완벽히 설정할 수 없는 경우가 대부분이다.(내_생각...) (ex> '학습 데이터에 오류--> target 못 구함' 정도..?)

따라서 조금씩 a를 변경하며 최적의 a값을 찾아나가는 과정을 한다.

이렇게 하면 위에 있는 학습 데이터에 오류가 있는 경우도, 해결가능하다.

------> delta a = L(E/x) : L 은 여기서 학습률이다. 완전히 값을 수정하는게 아니라 일부만 수정하는 것

3. 분류자는 하나가 아니다.

Bool 연산 : AND, OR, NOT, (XOR)

비가오고(and) 온도가 35도 이상이면 말라이아 가능성이 올라가나 아니면

비가오거나(or) 온도가 35도 이상이면 말라이아 가능성이 올라가나? 에 대한 답을 구하고자 할 때, 1가지 분류자로는 안된다. 

만약 비가 오고, 온도 35이상인 경우와, 둘다 부정인 경우에 가능성이 올라간다고 하면 절대로 1개로 분류자 못한다.

(이것은 XOR의 부정이다. NOT(XOR) or !XOR)

________________________________________________________________________________________________________________

본격적인 신경망

1. 뉴련 : 입력값이 분계점을 도달해야 출력이 발생한다. 

--> 인공 신경망 : 활성화 함수 중 시그모이드 함수(sigmoid function)을 사용하여, 분계점을 판단한다. 

sigmoid function > f = y = 1 / ( 1+e^(-x) )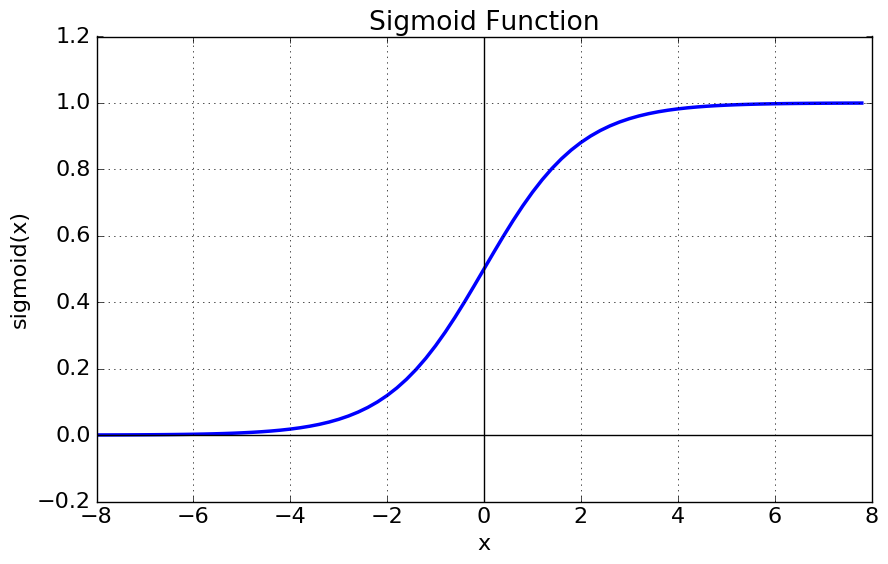

2. 뉴련 : 모든 입력의 합을 자신에게 오는 입력이라고 판단.

--> 인공 신경망 : 모든 입력의 합을 시그모이드 함수, 활성화 함수에 집어넣어 출력을 발생시킨다.

이때 각 뉴런을 노드라고 한다. 계층은 아래 그림 참고

이때 우리는 뉴련과 동일하게 하기 위해

(다음 뉴런에 도달한 정보의 세기가 분계점을 넘을 건지를 결정하는 것의 수 많은 모임으로 전체적으로 봤을때, (인간 뇌) 판단하게 함) 

노드 간 연결의 강도를 설정해야한다. 그리고 이때 쓰이는게 가중치(W)이다.

낮은 가중치는 신호를 약화하고, 높은 가중치는 신호를 강화한다. 

그리고 우리는 가중치를 수정함으로써, 학습시킨다.

그리고 하나의 노드는 프로그래밍 편의상 다음 계층의 모든 노드에 연결된다. 물론 더 창의적으로 구성할 수는 있다.

또, 역사적인 이유로, 첫번째 계층으로 가는 입력 값에는 가중치를 적용하지 않는다고 한다.

3. 행렬곱과 입력값 합 연산

행렬곱은 매우 가중치 연산에 편리하다. 

계층 2

에 들어오는 input 값, x는 다음과 같다.

X = sigma(k=1 to n(input개수) , input_K * W(이전,현재) ) 이다. //정확한 수식...

그리고 이건 행렬 곱으로 표현 가능하다.

(w1,1 w2,1)      (input1)        ( (input1 * w1,1 + input2 * w2,1) )

 *                    =

(w1,2 w2,2)      (input2)        ( (input1 * w1,2 + input2 * w2,2 ) )

로 되고

이건 위에 적은 X의 값과 일치한다. 

즉 우리는 앞으로 계층 2의 입력값을 

X = W(가중치 행렬) * I(입력값 행렬) 로 나타낼 수 있다.

그리고 계층 2가 마지막 이라면, O(출력 행렬) = sigmoid(X(입력행렬)이다.

계층 3

에 들어오는 input 값, x를 구해보자.